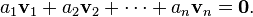MATRIZ DE TRANSICION

• Subestados Un estado puede descomponerse en subestados, con transiciones entre ellos y conexiones al nivel superior (superestado). Las conexiones se ven al nivel inferior como estados de inicio o fin, los cuales se suponen conectados a las entradas y salidas del nivel inmediatamente superior. Un ejemplo es el estado marcando de un teléfono (figura 5.5), que puede descomponerse en los subestados Inicio y marcado parcial.

Figura 5.5: Ejemplo de subestados

• Transición compleja Una transición compleja relaciona tres o más estados en una transición de múltiples fuentes y/o múltiples destinos. Representa la subdivisión en hilos del control del objeto o una sincronización. Se representa como una línea vertical de la cual salen o entran varias líneas de transición de estado. En el ejemplo de la figura 5.6 se muestra una transición a dos hilos concurrentes que luego se sincronizan.

Figura: Ejemplo de transición compleja

• Transición a estados anidados Una transición hacia un estado complejo, descrito mediante estados anidados, significa la entrada al estado inicial del subdiagrama. Las transiciones que salen del estado complejo se entienden como transiciones desde cada uno de los subestados hacia afuera, a cualquier nivel de profundidad. En la figura 5.1 se encuentran los dos casos nombrados: desde el estado inicial se pasa al estado Buen Funcionamiento (a su estado inicial) y de este estado salen transiciones hacia Mal Funcionamiento? y hacia el estado final, dichas transiciones deben comprenderse como transiciones de cada uno de los estados internos hacia los estados externos. Los diagramas de estado resultan adecuados para describir el comportamiento de un objeto a través de diferentes casos de uso, sin embargo, no resultan del todo adecuados para describir el comportamiento que incluye a una serie de objetos colaborando entre sí. Por lo tanto, resulta útil combinar los diagramas de estado con otras técnicas. Por ejemplo, los diagramas de interacción (4.1) son idóneos para la descripción del comportamiento de varios objetos en un único caso de uso, y los diagramas de actividades (5.2) muestran de forma adecuada la secuencia general de acciones en diferentes objetos y casos de uso. No nos debemos plantear el dise nar diagramas de estados para todas las clases en el sistema, sino sólo para aquellas que exhiban un comportamiento interesante de forma que la elaboración del diagrama de estados nos ayude a entender dicho comportamiento.

Sea una transformacion lineal es posible encontrar una matriz asociada a una transformacion lineal Desarrollo:

Si V y W son espacios de dimensi¨®n finita, y se eligen bases en estos espacios, entonces toda transformaci¨®n lineal de V a W puede ser representada como una matriz. Por otro lado, toda matriz real m por n determina una transformaci¨®n lineal de esta forma f(x) = Ax

Sea una base de V. Entonces todo vector v en V est¨¢ determinado de manera ¨ nica por los coefientes en : Si f : V ¡ú W es una transformacion lineal,

Lo cual implica que esto completamente determinada por los valores

Ahora es una base de W. Podemos representar cada f(vj) como

Entonces la funci¨®n f est¨¢ enteramente determinada por los valores ai,j.. Si se trata de transformaciones de generalmente se usa la base can¨®nica.

Si cambiamos las bases, entonces la matriz ser¨¢ distinta, pero representar¨¢ la misma transformaci¨®n

esta transformacion solo sirve en plano que sean de x,y,z para pasar a x,y

CAMBIO DE BASE

Cambio de base en espacios vectoriales y sus duales Sea un espacio vectorial de dimensión finita . Consideremos en una ``antigua base y una ``nueva base . Rigen unas relaciones:

 (1)

La matriz:

de tipo se llama la MATRIZ DE TRANSICIÓN DE LA ANTIGUA BASE #MATH2681# DE A LA NUEVA BASE . Puesto que es una familia linealmente independiente en , la matriz es una matriz inversible. Introducimos también las bases de duales de sendas bases de . Sea el único endomorfismo lineal de tal que:

 (2)



es de hecho un automorfismo lineal de . Ya que por (1) y (2):

la matriz de transición es la matriz del automorfismo con respecto a la antigua base de E. Aplicando el operador a ambos miembros de (1), obtenemos:

o sea, teniendo en cuenta (2):

 (3)

Estas fórmulas muestran que la matriz de transición es también la matriz del automorfismo con respecto a la nueva base de . Pasemos al automorfismo dual de . Por el teorema 2.2.6 las fórmulas (3) equivalen a:

 (4)

Por otra parte, en virtud de (2)

de donde:

 (5)

Comparando con (4), obtenemos la fórmula ``dual’‘ de (1):

 (6)

Al pasar de (1) y (6) notamos un ``doble fenómeno de inversión’‘, a saber: Las fórmulas (1) expresan los elementos de la nueva base de en función de la antigua base. Pero las fórmulas (6) expresan los elementos de la antigua base dual de en función de la nueva. En cada fórmula (1) se fija el índice inferior (índice de columna) de . Pero en cada fórmula (6) es fijo el índice superior (índice de fila) de ; o, si se quiere: La fórmula número en (1) pone en obra la columna número de .

La fórmula número en (6) pone en obra la fila número de .

DEPENDENCIA E INDEPENDEMCIA LINEAL

En álgebra lineal, un conjunto de vectores es linealmente independiente si ninguno de ellos puede ser escrito con una combinación lineal de los restantes. Por ejemplo, en R³, los vectores (1, 0, 0), (0, 1, 0) y (0, 0, 1) son linealmente independientes, mientras que (2, −1, 1), (1, 0, 1) y (3, −1, 2) no lo son, ya que el tercero es la suma de los dos primeros. Los vectores que no son linealmente independientes son linealmente dependientes.

Definición

Sea {v₁, v₂,..., v_n} un conjunto de vectores. Decimos que son linealmente dependientes si existen números 'a₁, a₂,..., a_n, no todos iguales a cero, tal que:

Nótese que el simbolo a la derecha del signo de igual no es cero, sino que simboliza al vector nulo. El conjunto de vectores nulos forma la matriz nula.

Si tales números no existen, entonces los vectores son linealmente independientes.

Utilizando conceptos de espacios vectoriales podemos redefinir la independencia lineal así:

Un conjunto de vectores U de un espacio vectorial es linealmente independiente si ∀

Esta idea es importante porque los conjuntos de vectores que son linealmente indepedientes y generan a un espacio vectorial, forman una base para dicho espacio.

Entre las propiedades de los vectores linealmente dependientes e independientes encontramos:

1. Un conjunto de vectores es linealmente dependiente si y solamente si alguno de los vectores es combinación lineal de los demás.
2. Si un conjunto de vectores es linealmente independiente cualquier subconjunto suyo también lo es.

Obviamente, si tenemos un conjunto de vectores tales que ninguno de ellos es combinación de los demás, escogiendo solamente unos cuantos, no podrán ser combinación de los otros.

1. Si un conjunto de vectores es linealmente dependiente también lo es todo conjunto que lo contenga.

Ya que un conjunto de vectores es linealmente dependiente si y solo si tiene algún vector que es combinación lineal de los demás, si metemos este conjunto de vectores en otro más grande, seguimos teniendo el vector que es combinación lineal de otros, por tanto, el conjunto más grande sigue siendo linealmente dependiente.

Significación geométrica

Geometricamente, dos vectores son independientes si no tienen la misma dirección (con sentidos idénticos u opuestos). Esta definición supone que el vector nulo tiene todas las direcciones.

Tres vectores son independientes si y solo si no están contenidos en el mismo plano vectorial, o sea si ninguno de ellos es una combinación lineal de los otros dos(en cuyo caso estaría en el plano generado por estos vectores).

El espacio generado por un sistema de vectores es el conjunto de todas las combinaciones lineales de estos vectores. Es un espacio vectorial. El espacio generado por un vector no nulo es la recta vectorial dirigido por este vector. El espacio generado por dos vectores independientes es el plano que los contiene. Resulta fácil comprobar que el espacio generado por un sistema de vectores es el menor (por la inclusión) espacio vectorial que los contiene a todos. Se le denomina vect A, donde A es el sistema de vectores. Si n vectores son independientes, el espacio generado es de dimensión n (dimensión en el sentido usual: 0 para un punto, 1 para una recta, 2 para un plano...).

Ejemplo

En el espacio tridimensional usual:

• u y j son dependientes por tener la misma dirección (y sentidos opuestos).
• u y v son independientes y definen el plano P.
• u, v y w son dependientes por estar los tres contenidos en el mismo plano.
• u v y k son independientes por serlo u y v entre sí y no ser k una combinación lineal de ellos o, lo que es lo mismo, por no pertenecer al plano P. Los tres vectores definen el espacio tridimensional.
• Los vectores o (vector nulo, cuyas componentes son iguales a cero) y k son dependientes ya que o = 0 ·k

Ejemplo del uso de la fórmula f:

¿Son los tres vectores siguientes independientes?

Buscamos tres valores x, y y z que satisfagan la ecuación:

Lo que equivale al sistema de ecuaciones siguiente:

Dado que la única solución es la trivial (x = y = z = 0), los tres vectores son independientes.

4.2 DEFINICION DE UN SUBESPACIO VECTORIAL Y SUS PROPIEDADES

Sub espacio vectorial:
Esto dice que si W es un sub conjunto del espacio vectorial V entonces este es un sub espacio de V. Si W es un espacio vectorial bajo las operaciones de suma y multiplicación por un escalar definidas en V.
Para que W sea un sub espacio de V debe cumplir las propiedades de cierre de la suma y la multiplicación por un escalar también debe cumplir la ley del elemento neutro bajo la suma, el inverso bajo la suma y el neutro bajo la multiplicación por un escalar.

TEMA 4.3 PROPIEDADES DE VECTORES, COMBINACION LINEAL, DEPENDENCIA E INDEPENDENCIA LINEAL.

Combinación Lineal:
Se denomina combinación lineal a u vector V en un espacio vectorial U u un cuerpo h.
Si los vectores v1, v2, v3, ..., vn en u si V puede expresarse como:
V = c1v1 + c2v2 + c3v3 +... + cnvn donde c son escalares del cuerpo h.
Envolvente Lineal:
Este es el conjunto de todas las combinaciones lineales semejantes denotado por Lin(v1, v2, ..., vn) y se denomina envolvente lineal de u1, u2, ...,un.
Siendo S un sub conjunto de un espacio vectorial V entonces Lin S es un sub conjunto de un espacio vectorial V y si W es un subconjunto de V que contiene a S, necesariamente Lin S es complemento de W.

4.1 ESPACIO VECTORIAL Y SUS PROPIEDADES

Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: escalarse (multiplicarlos por un escalar) y sumarse. Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.

Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices y sistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y complicada.

Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.

Motivación y definición

El plano R², consistente en los pares (x, y) de números reales, es el típico ejemplo de espacio vectorial: cualquiera dos pares de números reales pueden sumarse,

(x₁, y₁) + (x₂, y₂) = (x₁ + x₂, y₁ + y₂),

y cualquier par (x, y) puede escalarse, multiplicarse por un número real s, para obtener otro vector (sx, sy).

Existe además un vector, el (0,0), llamado vector nulo que cumple que al sumarse con cualquier otro vector no lo altera. Todo vector, por ejemplo el (1, 0), tiene su opuesto, el (-1, 0), que sumados dan como resultante el vector nulo (0, 0).

La noción de espacio vectorial es una generalización de esta idea. Es más general de varias maneras: en primer lugar, en lugar de los números reales otros cuerpos, como los números complejos o los cuerpos finitos, se permiten. En segundo lugar, la dimensión del espacio, que es de dos en el ejemplo anterior, puede ser arbitraria, incluso infinita. Otro punto de vista conceptual importante es que los elementos de los espacios vectoriales no suelen estar expresados como combinaciones lineales de un conjunto de vectores, es decir, no hay preferencia de representar el vector (x, y ) como

(x, y) = x · (1, 0) + y · (0, 1)

o como

(x, y) = (−1/3·x + 2/3·y) · (−1, 1) + (1/3·x + 1/3·y) · (2, 1)

3.1 DEFINICION DE MATRIZ

Se puede definir una matriz, como un conjunto de elementos (números) ordenados en filas y columnas.

Para designar una matriz se emplean letras mayúsculas. Cada uno de los elementos de la matriz (aij) tiene dos subíndices. El primero i indica la fila a la que pertenece y el segundo j la columna. Esta es una matriz de m filas y n columnas, es decir, de dimensión m x n. Esta matriz también se puede representar de la forma siguiente: A = (aij) m x n. Si el número de filas y de columnas es igual ( m = n ), entonces se dice que la matriz es de orden n.

2.4

2.1 , 2.2 y 2.3

2.1.- DEFINICIÒN DEL SISTEMA DE ECUACIONES LINEALES

Ecuaciones lineales con más de dos variables.

Para sistemas de ecuaciones lineales con más de dos variables, podemos usar el método de eliminación por sustitución o el método de eliminación por suma o resta (por adición o sustracción).

El método de eliminación por suma o resta es la técnica más breve y fácil de hallar soluciones. Además, lleva la técnica de matrices que se estudia en esta sección.

Cualquier sistema de ecuaciones lineales con tres variables tiene una solución única, un número infinito de soluciones o no tiene solución.

Método de eliminación para resolver un sistema de ecuaciones lineales:

Ejemplo:

Resuelve el sistema:

x + 2y + 3z = 9 …………………………….. (primer ecuación)

4x + 5y + 6z = 24 …………………………. (segunda ecuación)

3x + y - 2z = 4 ……………………………. (tercera ecuación)

Solución:

Suma −4 veces la “primera ecuación” a la “segunda”:

[x + 2y + 3z = 9]−4 → −4x −8y −12z =−36

4x +5y + 6z = 24

0 −3y - 6z = −12

Suma −3 veces la “primera ecuación” a la “tercera”:

x + 2y + 3z = 9

-3y - 6z = −12

-5y - 11z = −23

Multiplica por -(1÷ 3) la “segunda ecuación”:

x + 2y + 3z = 9

y + 2z = 4

-5y −11z = −23
Multiplica por −1 la “tercera ecuación”:

x + 2y + 3z = 9

y + 2z = 4

5y +11z = 23

Suma −5 veces la “segunda ecuación” a la “tercera”:

x + 2y + 3z = 9

y + 2z = 4

z = 3
Las soluciones del último sistema son fáciles de hallar por sustitución. De la “tercera ecuación”, vemos que z = 3. Al sustituir “z” con 3 en la “segunda ecuación”, y + 2z = 4 obtenemos y = −2. Por último, encontramos el valor de “x” al sustituir y = −2 y z = 3, en la “primera ecuación”, x + 2y + 3z = 9 con lo cual x = 4. Por tanto, hay una solución:

x = 4,

y = −2,

z = 3.
Sistema Matriz coeficiente Matriz aumentada

Antes de estudiar un método de matrices para resolver un sistema de ecuaciones lineales, daremos una definición general de matriz.

Definición de matriz.
Sean m y n enteros positivos. Una matriz de m x n (se lee “m” por “n”), es una matriz de la siguiente forma, donde cada aij es un numero real.

Ejemplos:






Sea la matriz:


por tanto, es una “matriz de orden 2 x 3.”

Sea la matriz:

por tanto, es una “matriz de orden 3 x 1.”

Teorema sobre transformaciones de renglones de matrices.

Dada una matriz de un sistema de ecuaciones lineales, resulta una matriz de un sistema equivalente si:

a) Se intercambian dos renglones. Símbolo: Ri Rj.

b) Se multiplica o divide un renglón por una constante diferente de cero. Símbolo: kRi Ri.

c) Un múltiplo constante de un renglón se suma a otro renglón. Símbolo: kRi + Rj Rj.

Uso de matrices para resolver un sistema de ecuaciones lineales.

Ejemplo.

Resuelve el sistema:

x + 2y + 3z = 9

4x + 5y + 6z = 24

3x + y - 2z = 4

Comenzaremos con la matriz del sistema, es decir, la matriz aumentada:

Luego aplicamos transformaciones elementales de renglón a fin de obtener otra matriz (más sencilla) de un sistema de ecuaciones equivalentes. Pondremos símbolos adecuados entre matrices equivalentes.

(−4)R1 + R 2 R 2

(−3)R1 + R 3 R 3?

(-(1÷ 3))R 2 R 2

(−1)R 3 R 3

(−5)R2 + R 3 R 3

Con la matriz final regresamos al sistema de ecuaciones:

Que equivale al sistema original. La solución x = 4, y = −2, z = 3 se puede encontrar ahora por sustitución.

La matriz final de la solución es una forma escalonada.

En general, una matriz está en forma escalonada si satisface estas condiciones:

a) El primer número diferente de cero de cada renglón, leyendo de izquierda a derecha, es 1.

b) La columna que contenga el primer número diferente de cero en cualquier renglón está a la izquierda de la columna con el primer número distinto de cero del renglón de abajo.

c) Los renglones formados enteramente de ceros pueden aparecer en la parte inferior de la matriz.

Ejemplo:


Sea la matriz:

es “una matriz escalonada”

Guías para hallar la forma escalonada de una matriz.

(a) Localizar la primer columna que contenga elementos diferentes de cero y aplicar transformaciones elementales de renglón a fin de obtener 1 en el primer renglón de esa columna.

(b) Aplicar transformaciones elementales de renglón del tipo kR1 + Rj Rj. para j > 1 y obtener 0 bajo el número 1 obtenido en la guía (a) en cada uno de los renglones restantes.

© Hacer caso omiso del primer renglón. Localizar la próxima columna que contenga elementos diferentes de cero y aplicar transformaciones elementales de renglón con objeto de obtener el número 1 en el segundo renglón de esa columna.

(d) Aplicar transformaciones elementales del tipo kR2 + Rj Rj. para j >2 y obtener 0 bajo el número 1 obtenido en la guía © en cada uno de los renglones restantes.

(e) Hacer caso omiso del primer y segundo renglones. Localizar la siguiente columna que contenga elementos diferentes de cero y repetir el procedimiento.

(f) Continuar el proceso hasta alcanzar la forma escalonada.

Uso de la forma escalonada para resolver un sistema de ecuaciones lineales.

Ejemplo:

Resuelve el sistema:

Solución: Comenzamos con la matriz aumentada y luego obtenemos una forma escalonada, según se describe en las guías.

R1 R4

R2 R3

(1)R1 + R 3 R 3

(−2)R1 + R 4 R 4

(−1)R 2 R 2

(-(1÷ 2))R 2 R 2

(−1)R2 + R 3 R 3

(−1)R2 + R 4 R 4

(3)R3 + R 4 R 4

La matriz final está en forma escalonada y corresponde a un sistema de ecuaciones:

(-(1÷ 2))R 4 R 4

Ahora usamos sustitución a fin de hallar la solución. De la última ecuación vemos que w = −1; de la tercera ecuación vemos que z = −2 . Sustituimos en la segunda ecuación, y obtenemos:

y - 2z - w = 6

y - 2(−2) - (−1) = 6

y + 4 + 1 = 6

y = 1

Sustituimos los valores encontrados en la primera ecuación:

x + z + 2w = −3

x + (−2) + 2(−1) = −3

x - 2 - 2 = −3

x = 1

Por lo tanto, el sistema tiene una solución: x = 1, y = 1, z = −2, w = −1.

2.2 CLASIFICACION DE LOS SISTEMAS DE ECUACIONES LINEALES Y TIPOS DE SOLUCION.

Los sistemas de ecuaciones se clasifican en 3 tipos:los que tienen infinitas soluciones, los que tienen una solucion y los que no tienen solucion.

Tienen soluciones infinitas cuando las rectas del sistema de ecuaciones son paralelas.

Tienen una solucion cuando las rectas del sistema de ecuaciones se intersectan.

No tienen solucion cuando estan una sobre otra en las rectas del sistema de ecuaciones.

2.3 INTERPRETACION DE LAS SOLUCIONES GEOMETRICAS.

La ecuación de segundo grado y sus diversas soluciones tienen una traducción al campo gráfico muy interesante y esclarecedora. Recuerda que la parábola es una línea curva representativa de la función polinómica .

Cuando la y=0, la parábola corta al eje de abscisas; a su vez, la expresión anterior queda reducida a . Luego las soluciones de la ecuación de segundo grado son los puntos de corte de la parábola asociada con el eje de abscisas. Por tanto, una ecuación de segundo grado tiene tantas soluciones reales como veces corte la parábola asociada a ella al eje de abscisas.

3. Pinta en la siguiente escena las parábolas asociadas a las ecuaciones del ejercicio 1y comprueba lo dicho en el párrafo anterior. La escena empieza con la resolución gráfica de la ecuación , su discriminante vale 1 y, por tanto, tiene dos soluciones reales distintas, que son 2 y 3.

Ejercicios a resolver

1.5 Teorema de Moivre, potencias y extraccion de raices de un numero complejo.

Abraham de Moivre-(Historia)


Teorema de Moivre-(Utilizando el principio de inducción matemática mostraremos que:)

Leonhard Paul Euler-(Historia)

Dado que la textura del Universo es la más perfecta y la obra de un Creador sapientísimo, nada sucede en el Universo sin obedecer alguna regla de máximo o mínimo.

1.4 Forma Polar y Exponencial de un Numero Complejo

ARGAND
Fue un contable y matemático suizo que describió en 1806 la representación geométrica de los números complejos, creando lo que se conoce como plano de Argand.

En matemáticas, el plano complejo es una forma de visualizar el espacio de los números complejos. Puede entenderse como un plano cartesiano modificado, en el que la parte real está representada en el eje x y la parte imaginaria en el eje y. El eje x también recibe el nombre de eje real y el y eje imaginario


Un número puede ser visualmente representado por un par de números formando un vector en un diagrama llamado diagrama de Argand
El plano complejo a veces recibe el nombre de plano de Argand a causa de su uso en diagramas de Argand. Su creación se atribuye a Jean-Robert Argand, aunque fue inicialmente descrito por el encuestador y matemático Noruego-danés Caspar Wessel.
El concepto de plano complejo permite interpretar geométricamente los números complejos. La suma de números complejos se puede relacionar con la suma con vectores, y la multiplicación de números complejos puede expresarse simplemente usando coordenadas polares, donde la magnitud del producto es el producto de las magnitudes de los términos, y el ángulo contado desde el eje real del producto es la suma de los ángulos de los términos.
Los diagramas de Argand se usan frecuentemente para mostrar las posiciones de los polos y los ceros de una función en el plano complejo.
El análisis complejo, la teoría de las funciones complejas, es una de las áreas más ricas de la matemática, que encuentra aplicación en muchas otras áras de la matemática así como en física, electrónica y muchos otros campos.


POTENCIA
La potenciación es una operación matemática, que se nota como an, y que se lee "a elevado a n", que involucra dos números: la base a y el exponente n. Su definición varía según el conjunto numérico al que pertenezca el exponente:
• Cuando el exponente es un número natural, la potenciación corresponde a una multiplicación de varios factores iguales: el exponente determina la cantidad de veces que la base se multiplica por sí misma. Por ejemplo:
• 24 =2.2.2.2=16. En general:
an =ax…xa
• cuando el exponente es un entero negativo -p, una potencia que tenga exponente negativo es el resultado de elevar la fracción inversa de la base 1/a al exponente positivo p.

a-p =1/ap
La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales.
Como caso especial, destacar que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 00, en principio, no está definido (ver en Cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacío o simplemente por analogía con el resto de números.

1.2 Operaciones fundamentales con numeros complejos

1.1 Definicion y Origen de los Numeros Complejos, 1.2 Operaciones Fundamentales con Numeros Complejos